Instructions for the Lab Session Report:

Normal Equation and Batch Gradient Descent Methods

Dear Student ,📚📝✨

 

This lab session is designed to deepen your understanding of linear models by requiring the development of a comprehensive technical report on the normal equation and batch gradient descent methods in linear multiparametric models. The report should provide a rigorous exploration of these approaches, highlighting their theoretical foundations, computational characteristics, and practical implications.

 

---

Theoretical overview

Normal Equation

The normal equation (NE) provides a closed-form solution for linear regression by directly computing the optimal model parameters. This approach is computationally efficient for small datasets but becomes impractical for large datasets due to the significant computational cost associated with matrix inversion.

Batch Gradient Descent and Its Variants

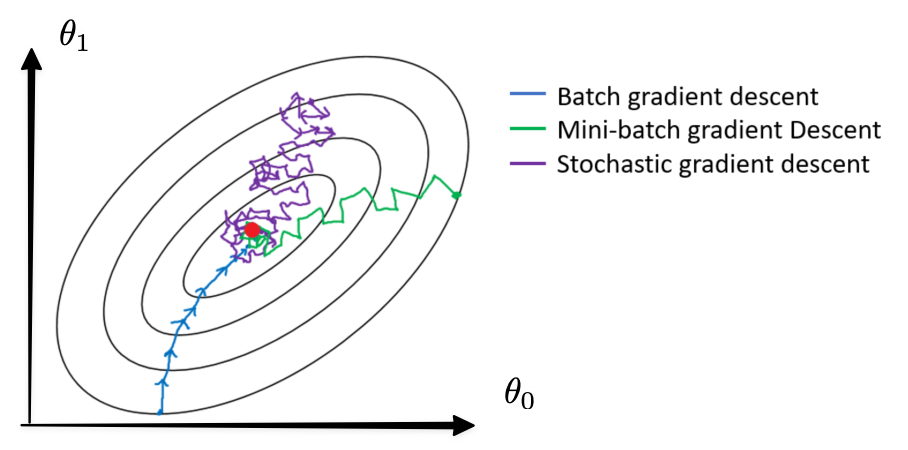
Gradient descent is an iterative optimization algorithm that adjusts model parameters to minimize the cost function (J). It is particularly well-suited for large datasets, as it updates parameters incrementally. The three primary variants of gradient descent are:

• Batch Gradient Descent (BGD): Updates parameters using the entire dataset in each iteration.

• Mini-batch Gradient Descent (MBGD): Utilizes a subset of the data (mini-batch) for parameter updates.

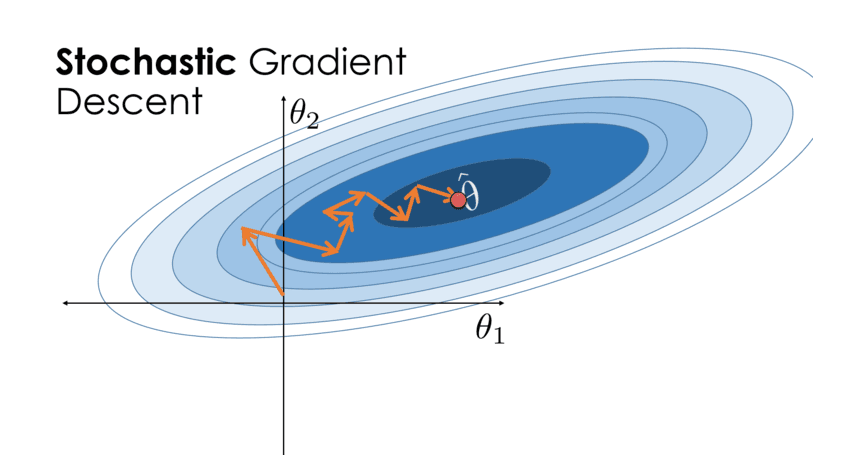
• Stochastic Gradient Descent (SGD): Updates parameters using a single, randomly selected data instance per iteration.

These methods necessitate careful selection of hyperparameters, particularly the learning rate, to ensure stable convergence and avoid a local minimum.

 

---

Objectives and Required Tasks

Students are expected to conduct independent research, implement the discussed methods, and submit a structured report detailing their findings and results. Thus, the report development must consider the following points (points marked ☑️ are student's tasks) :

1. Theoretical Background

• ☑️ Provide a detailed theoretical discussion on the normal equation and gradient descent methods in your report's theoretical section.

• Use LaTeX to formally present the mathematical derivations for:

  • ☑️ The Normal Equation (NE).

  • ☑️ The deterministic method of Batch Gradient Descent (BGD) applied to multiparameter linear models.

2. Dataset Utilization 💾

• Utilize the dataset provided in the designated repository.

3. Implementation of the Normal Equation

• ☑️ Develop a multiparametric linear regression model based on the dataset and analyze the computed model parameters for y=θ₀+θ₁ x₁.

• ☑️ Extend your model to y=θ₀+θ₁ x₁+θ₂ x₂.

4. Implementation of Gradient Descent Methods

• ☑️ Implement Batch Gradient Descent (BGD) for the given three datasets.

• ☑️ Implement Mini-batch Gradient Descent (MBGD):

  • Experiment with various mini-batch sizes (e.g., 5-10, 20, and 30).

• ☑️ Implement Stochastic Gradient Descent (SGD):

  • Select a single random instance per iteration for parameter updates.

• ☑️ Track the Mean Squared Error (MSE or J) performance throughout the iterations.

• ☑️ Implement a plotting feature to visualize the progression of the MSE (J).

• Adjust the scaling of axes to highlight parameter evolution across iterations.

5. Visualization of Parameter Evolution (only for two-parameter model)

• ☑️ Determine optimal hyperparameters for each method.

• ☑️ Generate parameter trajectory plots with:

  • x-axis as θ₀

  • y-axis a θ₁

  • Analyze the convergence behavior of the models during each iteration; try to use the same number of iterations to compare the evolution of three methods and their final values. 

 

 

6. Conclusions ☑️

• Compare the efficiency, accuracy, and computational complexity of the normal equation and gradient descent methods.

• Discuss the impact of dataset size, hyperparameters, and MSE behavior on methods performance.

---

Submission Guidelines

1. Report Formatting and Naming Convention

• Submit the report in PDF format, compiled using LaTeX. 

• Use as guide the LaTeX report format.

• Adhere to the following file naming convention:

  • [Student1]-[Student2]-LabSession-[Date].pdf
    (Example: John-Peter-NEBGD-Oct30.pdf)

2. Submission Deadlines 📅

• Monday Lab Session: October 13th (by 11:59 PM, via OwnCloud)

3. Quality Assurance Before Submission

• Verify the completeness and correctness of responses.

• Proofread to eliminate spelling and grammatical errors.

• Ensure proper implementation and adherence to formatting guidelines.

---

Recommendations for Effective Completion

• Organized Workflow 📂: Maintain a structured repository for assignments and create backups.

• Clarification Requests: Address any uncertainties with the instructor well before the deadline.

• Early Preparation ⏰: Commence work promptly to allow sufficient time for research and troubleshooting.

• Regular Updates 📩: Monitor email correspondence for potential modifications to the requirements.

---

 

Happy coding!

Gerardo Marx,

Lecturer of the Artificial Intelligence and Automation Course,

gerardo.cc@morelia.tecnm.mx